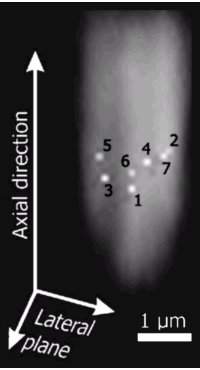
The formulation of a criterion for resolution by Lord Rayleigh in 1879 states that two point sources of light are resolvable if their mutual distance in image space is not smaller than the radius of the first dark ring around the central disk of the Airy diffraction pattern related to the two sources. In object space this corresponds to the FWHM of the microscope Point Spread Function (PSF). For perfect optical systems, this distance cannot be smaller than roughly wavelength/2 (of the mediating lightwave) for the lateral dimension. This limit is called the Abbe limit. It is still possible, however, to locate and visualize two tiny objects such as fluorescing molecules with a mutual distance much smaller than this limit using far field optics. In order to accomplish this we make use of the fact that the individual molecules have slightly different 0-0 transition energies. By using a single-mode laser with very narrow bandwidth (~1 MHz) we can spectrally resolve each molecule within the confocal detection volume, given small homogeneous linewidths and spectrally stable zero-phonon lines of the molecules, as well as negligible dipole-dipole interaction between them. Using a confocal microscopy setup we can image the red-shifted fluorescence of each separate molecule onto a CCD camera. Their lateral positions in image space are then given by the center of the resulting 2-D spatial distribution of photons. The magnification factor of the microscope gives their separation in object space. We redefine resolution in this case to mean the reproducibility with which the spatial position of each imaged emitter can be determined. This is not limited by the imaging optics, but by the photo-stability and the fluorescence count rate of the molecules combined with the mechanical stability of the microscope. It is also possible to determine the axial position of the emitting molecule (with smaller accuracy) by shifting the position of the CCD camera along the optical axis.
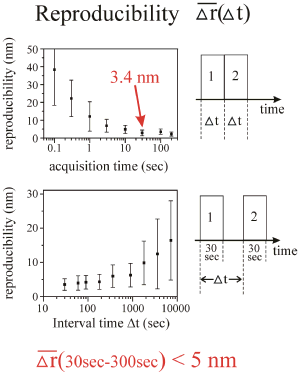
When the collected signal becomes larger, the error due to photon counting statistics becomes smaller. On the other hand, a larger signal for the same molecule means longer acquisition times, increasing the impact of mechanical fluctuations. If we take the difference of the positions for two successively recorded images as a measure for the reproducibility, we can use this to quantify the two influences. Measuring reproducibility many times for different acquisition times, yields an optimum for roughly 30 s at a reproducibility of 3.4 nm. No deterioration due to mechanical drift is observed even after acquisition times of 200 s. At the optimal value of 30 s the influence of the mechanical drift is such that for measuring times shorter than 10 min the relative position of single molecules can be determined with a precision of better than 5 nm. This is two orders of magnitude below the Abbe limit. Even after interval times longer than several hours a reproducibility better than 30 nm is obtained without any drift correction.
- A.M. van Oijen, J. Köhler, J. Schmidt, M. Müller, G.J. Brakenhoff
“3-Dimensional super-resolution by spectrally selective imaging”
Chem. Phys. Lett. 292 (1998) 183-187 - A.M. van Oijen, J. Köhler, J. Schmidt, M. Müller, G.J. Brakenhoff
“Far-field fluorescence microscopy beyond the diffraction limit”
J. Opt. Soc. Am. A 16 (1999) 909-915 - A. Bloeß, Y. Durand, M. Matsushita, H. van der Meer, G.J. Brakenhoff, J. Schmidt
“Optical far-field microscopy of single molecules with 3.4 nm lateral resolution”
J. Microsc.-Oxf. 205 (2002) 76-85