Electromagnetic waves
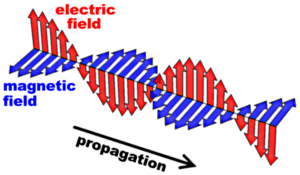
Many of the observable properties of light can be understood if it is regarded as a wave which travels with a finite speed c (3 x 108 m/s). James Clerk Maxwell could show that equations which he had derived to describe the behavior of time-varying electric and magnetic fields predicted the existence of propagating waves and his theory yields precisely the speed of light (known from measurements) as their velocity. The picture to the right shows a “snapshot” of such an electromagnetic wave: The red and blue arrows symbolize an electric and a magnetic field, respectively, which are perpendicular to one another. The strength of these fields varies along the propagation path; this is indicated by the lengths of the arrows. Both these fields also vary in time and this leads to the propagation of the wave. (Clicking on the image links to an animated version of the wave; maybe this helps to visualize the concept.)
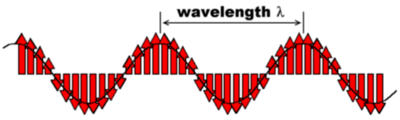
Two important parameters to characterize an electromagnetic wave are its wavelength ? and its frequency ?. The wavelength ? is the shortest distance between two points along the propagation path at which the electric field strength is the same at any given moment. This is illustrated in the next figure:
(We have neglected the magnetic field since it is often sufficient to consider only the effect of the electric field on e.g. molecules.) The human eye can see electromagnetic waves with a wavelength between 400 nm (blue) and 800 nm (red).
The frequency of the electromagnetic radiation is a measure for how fast the electric and the magnetic field oscillate; i.e. how many times per second they change their direction for any point along the propagation path. The fact that the wave has to travel exactly one wavelength during one oscillation period (in order to retain its periodicity in space and time) requires that the product of its wavelength ? and its frequency ? is equal to the propagation speed c. The wavelength range given above for visible light therefore corresponds to frequencies between 3.75 x 1014 (red) and 7.5 x 1014 (blue) oscillations per second.
An important consequence of the wave character of light should be mentioned here already, since it will become important later on: By focusing light with normal optics one cannot achieve spot sizes significantly smaller than its wavelength; likewise, it is impossible to optically resolve structures on lengthscales much smaller than the wavelength in a normal imaging apparatus. (We will define more precisely what “normal” optics are in the chapter about the principles of optical microscopy.)
Photons
Even though the Maxwell’s electrodynamic theory is very successful in explaining the properties of light, it cannot account for all experimental observations. Famous historic examples for this are the radiation spectrum of a black body and the photo-electric effect. Both these phenomena (and many more) can only be understood if one assumes that the energy in a radiation field is quantized in discrete steps, which is a contradiction to the model of “smooth” electromagnetic waves. These “grains” of energy are called photons. In the end it will depend on the nature of the experiment whether light will show either its wave character or its photon character, and it will never be both at the same time. This notion – the principle of complementarity – is quite at odds with “common sense”, but this type of common sense is derived from our everyday experiences in the macroscopic world and is hence not well-suited to understand phenomena at the nanometer scale.
The photon picture is often very convenient to describe the interaction of light with molecules: The energy of a photon is proportional to the frequency of the radiation (and inversely proportional to its wavelength). When a photon “hits” a molecule, it can change the molecule’s state in various ways, provided that it carries enough energy to access one of the allowed excited states of the molecule. (Yes, those are energy-quantized as well.) Optical spectroscopy makes use of this fact by recording the wavelength-dependent reaction of molecules (and other quantum systems) to irradiation with light and drawing conclusions about the particles’ internal energy levels and their structure from the results. This will be explored in greater detail in the next chapter.